![]()
![]()
![]() Previous: Numerical integration techniques
Up: Numerical Theory
Next: Runge-Kutta formula/derivation
Previous: Numerical integration techniques
Up: Numerical Theory
Next: Runge-Kutta formula/derivation
The most straightforward way to generate an easily integrated
approximation for 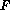 is to take a Taylor series expansion of
it,[2][pages 240-241]
terminating the expansion after some predetermined number of terms.
is to take a Taylor series expansion of
it,[2][pages 240-241]
terminating the expansion after some predetermined number of terms.
The error due to terminating the series is proportional to the
first term dropped. Terms of higher order will contribute less than
lower order terms.![]()
When 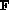 is used directly in place of
is used directly in place of  (that is,
only the first term is kept), the technique becomes the first order
Euler method.
(that is,
only the first term is kept), the technique becomes the first order
Euler method.
Typically, a higher order approximation will result in a more accurate
approximation, however to use a Taylor sequence of order  , requires
that the function be
, requires
that the function be  times differentiable. Looking at the force
function in equation
times differentiable. Looking at the force
function in equation ![]() , one can see that the function is
not easily differentiable. It is, in fact, two valued, due to the
absolute value operation required to define the direction vector.
Further, for very small distances, the denominator may become zero
(due to underflow), and cause a singularity.
, one can see that the function is
not easily differentiable. It is, in fact, two valued, due to the
absolute value operation required to define the direction vector.
Further, for very small distances, the denominator may become zero
(due to underflow), and cause a singularity.
mcr@ccs.carleton.ca