![]()
![]()
![]() Previous: Taylor sequences
Up: Numerical Theory
Previous: Taylor sequences
Up: Numerical Theory
The Runge-Kutta method has the desirable property of not requiring actual evaluation of the derivatives. The precise form of the function is often not known, or may be very costly to evaluate. A Runge-Kutta method is formed by approximating the second order Taylor polynomial
(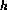 is the step size) by
is the step size) by 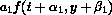
This is done in [2][pages 242-243], and the highlights follow below.
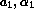 and
and  , Taylor expand
, Taylor expand
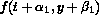 :
: 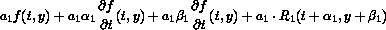 where the remainder term is
where the remainder term is
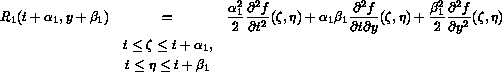
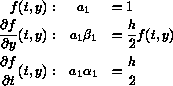
This results in the Midpoint method given by
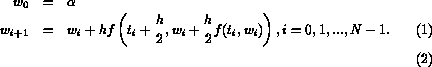
Note, the remainder term 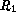 is
is 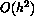 , making the Midpoint method
a second order method. This means that the function being integrated
is being approximated by a parabola at each step.
, making the Midpoint method
a second order method. This means that the function being integrated
is being approximated by a parabola at each step.
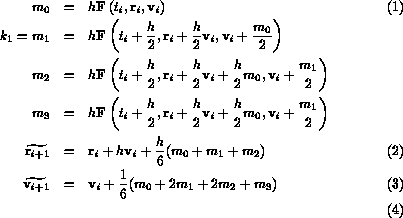
With two approximations, the quality of the approximation [2][page 271] is given by
This quality factor can be used to increase or decrease the value of
the step size.  is the tolerance desired. The new step size
is given by
is the tolerance desired. The new step size
is given by 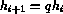
mcr@ccs.carleton.ca